DATA SCIENCE USING PYTHON

ONLINE TRAINING COURSE

The basic assumption of the time series analysis is that the factors that have influenced patterns of the activity in the past and present will continue to do so in more or less the same manner in the future. It means that, the factors affected in past or present, the same factors are going to affect in the future.

Here, the aim is to identify and isolate the influencing factors for predictive/forecasting purposes.

The question is what are those factors?

Before, we discuss the factors; let me get the one time series plot on some data.

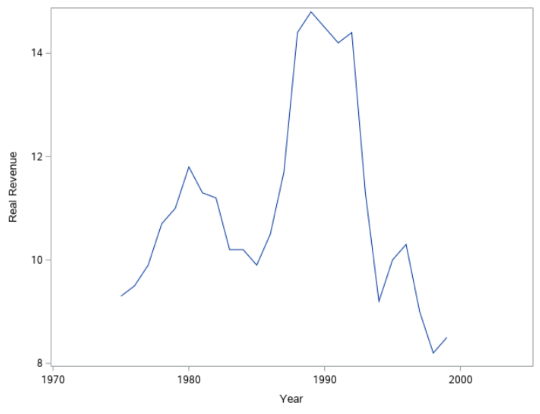
As clearly seen this graph that, Real revenue is not constant across the years. There are below factors affecting the revenue (up and down) across the time (here, year).

Component	Classification	Definition	Reason of Influence	Duration
Trend	Systematic	Overall or persistent,long-term upward or downward pattern of movement	Changes in technology, wealth, population.	Several Years
Cyclical	Systematic	Repeating ups and down swings through four phases: peak to recession to depression to recovery/growth	Different economical factors	Usually 2 to 10 years
Seasonal	Systematic	Fairly regular periodic fluctuations that occur within each 12 months period	Weather condition, social customs, religious customs, school/college schedules and so on.	Within 12 months(or monthly or quartly data
Irregular	Unsystematic	The residual fluctuations in a series that exist after taking into account all above systematic effects	Random variation in data due to unforseen events like strike, wars and so on.	Short duration and non repeating

So, based on all above factors, any time series is a product of these components.

For Annual Time Series:

Yi = Ti × Ci × Ii
Y = observed value at time i
T = Trend component at time i
I = Irregular component at time i

For Monthly or Quarterly Time Series:

Yi = Ti × Ci × Ii × Si
Y = observed value at time i
T = Trend component at time i
I = Irregular component at time i
S = Seasonal component at time i

Okay!!! We have enough knowledge about what it time series analysis and why it is important in any business.

Before we start the looking into forecasting models, let me set up case study in order to relate to any of the forecasting models.

CASE STUDY:

Problem Statement: Forecast the revenues of three companies (Eastman Kodak, Cabot Corporation and Wal-Mart) in order to better evaluate investment opportunities for your client.

Domain/Role: Financial Analyst

Topics: Moving Average, Exponential Smoothing, Trend Fitting Models and ARIMA